Wheels Vs. Doors: The Great Debate, Solved Mathematically

Gavin Herrmann and Tate McDonald|April 1, 2022

The calculations that went into solving this question were complicated and many.

Credits to Tate McDonald for calculations

The great discussion between wheels and doors has raged on for years, however, it has recently risen in popularity and diehard supporters can be found on either side of the argument as to whether there are more doors or wheels.

Through extensive research, I’ve calculated which side is correct, finally laying this great battle to rest. To begin, in August of 2017 there was a solar eclipse near where I live. I was able to see almost a full eclipse, but was not quite in the full shadow of the moon so did not get to experience the full eclipse. Since then I have seen pictures of the total solar eclipse, and have longed to see it in person. Along with that I have always been completely fascinated by outer space and the planets of our solar system, so when it came time to choose a topic for my IA I knew it had to be something space related, and then I remembered the fascination I had with solar eclipses and the topic came to mind right away. It was a perfect way to encompass my interests as well as allowing for mathematical studies.

Aim: to find how often the most optimal solar eclipse occurs using parametric vectors and calculus to find orbital periods and velocities

Background

In 1609 German astronomer Johannes Kepler formulated three laws to explain planetary motion. The first law states that all planets travel in an ellipse with the sun at one foci, which is the main law used in this investigation. The second law states that a planet will sweep out the same area over equal amounts of time. And the third law states that the square of the period of orbit is directly proportional to the cube of the radius. These laws directly modeled what happened at a planetary level, but failed to predict why these things happened. Later in 1666 Newton formulated his law of universal gravitation, which predicted a force of attraction between any 2 objects in the universe. This theory explained Kepler’s laws and with the creation of calculus, Newton was able to model the laws better.

Solar eclipses happen very frequently across earth, when the moon is directly in between the sun and the earth and casts a complete shadow called the umbra and a partial shadow called the penumbra. The main driving force is how the planets and moon revolve around each other. The moon revolves around the earth in a very circular orbit, just like how the earth moves in a very circular orbit around the sun. The orbits are still elliptical with a small eccentricity. Other objects such as Pluto and many comets have much more elliptical orbits with higher eccentricity. It is important to be able to know the orbits of planets and other celestial bodies, so that astronomical events can be predicted like the path of an asteroid or solar and lunar eclipses.

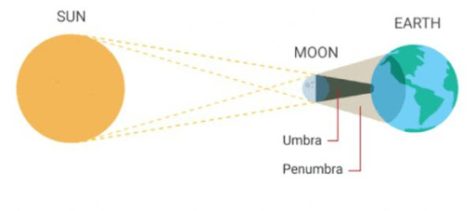
For this investigation it is assumed that the moon and earth are revolving on the same plane, whereas in actuality the moon has a slightly tilted orbit about 5.1°. This assumption will provide errors in my calculations and for further investigations should be considered. It is also assumed that the most optimal solar eclipse position will be when the moon is closest to the earth and the sun is farthest from the earth so that the moon appears larger and the sun smaller.

Term Definitions

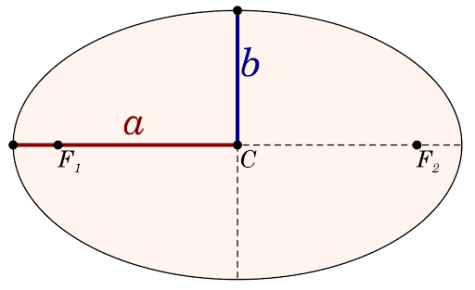
Ellipse: a type of conic shape similar to a circle but without a constant radius

Eccentricity: the measure of how elliptical an ellipse is 0<e<1 with 1 being a parabola, greater than 1 being a hyperbola, and 0 being a circle

Focus: there are two points on the Semi major axis where the sum of the distance of any point, on the ellipse, from these two points, is constant

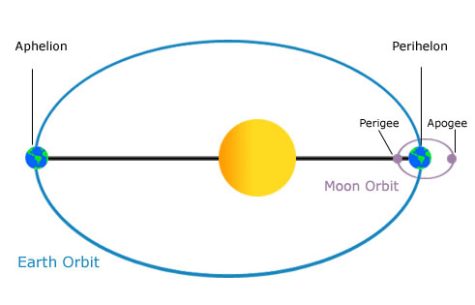
Apogee: the point at which the moon or a satellite is farthest from the earth

Perigee: the point at which the moon or a satellite is closest to the earth

Semi major axis: the distance from the center of the ellipse to the longer part of the ellipse commonly denoted as a

Semi minor axis: the distance from the center of an ellipse to the shorter part of the ellipse, commonly denoted as b

Aphelion: the point at which a planet, asteroid, or comet is the farthest from the sun

Perihelion: the point at which a planet, asteroid, or comet is the closest to the sun

Equations:

Parametric:(cost,sint)

Focus: c2=a2–b2

Orbital Velocity: v=GM/r

ddxs(t)=v(t)

s(t)=(x(t),y(t))

v(t)=(x'(t),y'(t))

baGMrdra-b=vavg

L=ab(dxdt)2+(dydt)2dt

T=Cvavg

Calculations

Modeling Orbital Path of the Moon

Based on Kepler’s first law of motion we know that all celestial bodies orbit in an ellipse which can be modeled by a parametric function:

(acos(t),bsin(t))

with a being the semi major axis and b being the semi minor axis, which are 384400 km and 383800000 km respectively so that the function is:

(384400cos(t,)383800sin(t))

This gives the function of an ellipse with the earth at the center, however the earth is located at one of the foci of to moons path meaning that we have to factor the focus distance in which is given by: c2=a2–b2 with c as the focus thus we get:

c2=3844002-3838002

c=3844002-3838002 so c=21469.04749km

Thus a transformation to the right is performed with

(384400cos(t)+21469.04749,383800sin(t)), which gives us the model: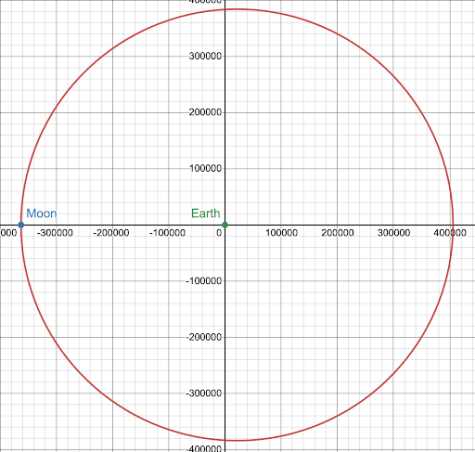

Next I found the velocity and circumference of the moon’s orbit to find the period or time it takes to orbit the earth with the equation t=dvrearranged from v=dt where v is the average velocity, d is the distance or circumference, and t is the time. The parametric equation above is in the form of a position vector: s(t)=(x(t),y(t)), and which velocity is given by: v(t)=(x'(t),y'(t)), since velocity is the derivative of positionddxs(t)=v(t)

For orbital velocity the following equation is given: v=GM/r where G is Newton’s Universal Gravitation constant G=6.67*10-11m3kg-1s-2and M is the Mass of the earth at5.972*1024kg. The radius of the earth-moon system is always changing because of the elliptical orbit of the moon and at the farthest position from the earth(apogee) the distance is found using Semi major axis+c384400+21469.04749=405899.0475km. And at the shortest distance(perigee) the distance is Semi major axis-c384400-21469.04749=362930.9525km.

Plugging these values into v=GM/r we find that at apogee the velocity is 990.635ms-1and the velocity at perigee is 1047.635ms-1.

To find the average velocity that the moon travels the following equation is given:

383800000384400000GMrdr384400000-383800000=vavg

3838000003844000006.6710-11*5.9721024rdr600000

3838000003844000003.9833241014rdr600000=1018.358508ms-1

The integral from the perigee to the apogee gave the velocities added up, and dividing by the difference of apogee and perigee the average velocity was obtained.

Finding Circumference of the Moon’s Orbit

Finding the circumference of an ellipse is difficult due to the fact that there is not a constant radius for the orbit, and so to find the circumference I used the Length equation: L=ab(dxdt)2+(dydt)2dt

To use this equation however, I needed dxdt and dydt, when there was only x(t) and y(t) in the parametric form. In other terms, dxdt and dydt are the derivatives of the parametric position vectors, and thus to obtain these we have to get the parametric velocity vector or the derivative of the position vector s(t).

s(t)=(384400cos(t)+21469.04749,383800sin(t))

ddts(t)=v(t)=(ddt(384400000cos(t)+21469.04749),ddt(383800000sin(t)))

(-384400000sin(t),383800000cos(t)), since ddxcost=-sint and ddxsint=cost

Then by plugging x'(t)and y'(t) into L=ab(dxdt)2+(dydt)2dt from 0 to 2π

L=02(-384400000sin(t))2+(383800000cos(t))2dt and by solving

L=2413371845m

Finding orbital Period

Using the equation T=Cvavgderived from v=dt where v is the average velocity, C is the distance or circumference, and T is the orbital period in seconds. It is possible to plug in the numbers from previous sections. To get

T=24133718451018.358508=2369864.666s

To get the period in terms of days:

2369864.666*160*160*124=27.42898918 days

Thus the moon takes 27.42898918 days to orbit the earth, so assuming that the moon starts at perigee, which is the optimal position for a solar eclipse on earth, it will return to that spot every 27.42898918 days.

Modeling the Earth, Moon, Sun System

For the Sun, Earth, Moon system the earth orbits with a semi major axis of 149.6106km and a semi minor axis of 149.5576999826106km making it a very circular orbit even more so than the moon around the earth with an eccentricity of 0.0167.

From this we can model the system in the same way we did above by using parametric equation:

(149.6106cos(t),149.5576999826106sin(t))

And finding the focus, c2=3844002-149.5576999826106

c=149.59788751062-149.5769998261062 so c=2499813.49613km

Thus we get the parametric equation: ((149597887.5cost)+2499813.49613, 149576999.826sin(t)), which is shown in the following model:

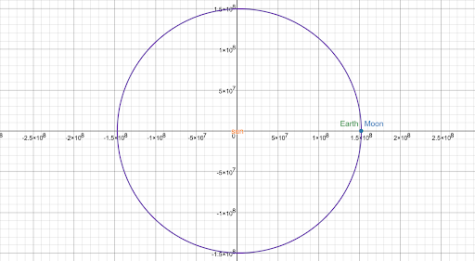
Conclusions:

The results of this study seem to be around 59,000 ms-1Mpc-1. This value is lower than the widely accepted 64,000ms-1Mpc-1This is a topic that has been much debated among scientists. Hubble originally calculated the rate of expansion to be about 500 ms-1Mpc-1, and later it was revised to 74ms-1Mpc-1and 67.8ms-1Mpc-1. Different methods used resulted in different values.

Errors:

Despite this massive variety in conclusions, there were most likely methodological errors made along the process of this study. The distances are found by measuring the luminosity of these supernovae and comparing it to the expected luminosity. There is not complete certainty about the expected luminosity of these type Ia supernovae.

There is also likely error within these distances as they are approximate distances and were calculated through the use of other data points. Also in space there are many gases and dust clouds that could cause a dimming of light from these Supernovae as they travel to earth, which would contribute to a large error. There was likely error within the method as well, and possibly using a smaller diversity of supernovae could have caused issues with the methodology.

Extension:

In order to continue research in this study more precise data points would be needed and there would be other methods used. The exact distances, redshift, and recessional velocities would be needed to get a more accurate result, as any small variation can largely skew the data. I would also need to know what the light from these supernovae traveled through to determine if there is anything that could have disrupted the travel. Another way to continue and make the results more accurate, would be to use the other methods used today and compare the different results. Also the use of more diverse data points, some very close to our perspective, and some very far away from our perspective would be needed to get a more accurate line after graphing, and thus get a more accurate value for the expansion of the universe.

This data and the calculations accompanying them serve to finally end the debate about whether there are more doors or wheels on planet earth.

Bibliography

Castelvecchi, Davide. “How fast is the Universe expanding? Cosmologists just got more confused.” Nature. Accessed November 18, 2021. https://www.nature.com/articles/d41586-019-02198-z.

Central Bureau for Astronomical Telegrams. http://www.cbat.eps.harvard.edu/.

Chen, Hyaline. “Calculating the expansion rate of the universe.” YS Journal. Last modified September 27, 2020. Accessed November 18, 2021. https://ysjournal.com/calculating-the-expansion-rate-of-the-universe-2/.

Open Supernova Catalog. https://sne.space/.

Richmond, Michael. A connection between radial velocity and distance. Accessed November 18, 2021. http://spiff.rit.edu/classes/phys240/lectures/expand/expand.html.

Supernova Recessional Velocity and Redshift Data. Table. Asiago Supernova Catalog. Accessed November 18, 2021. http://cdsarc.u-strasbg.fr/viz-bin/nph-Cat/txt?B/sn.

Warren, Sasha. “The Hubble Constant, Explained.” Uchicago News. Accessed November 18, 2021. https://news.uchicago.edu/explainer/hubble-constant-explained.

Super Nova used: